Newton's Cradle - Enery is always conserved somewhere

24 Sep, 2022 - Funnel Edu World Physics

Energy is always conserved somewhere. We just need to bring it in a usable form to get some work done.

Let's understand with Newton's cradle.

It is one of the best practicals to understand the #Conservation of #Momentum (Mass & velocity) & #Energy. But what excites me most is the 3rd ball of the 5 ball cradle. If you swing 3 balls, it will hit the 2 balls at rest. The 3rd ball which hits joins the 2 and moves with them. This continues...

Did you notice the middle ball remains always in motion while the side 2 ball goes on rest alternatively?

The conservation of momentum (mass × velocity) and kinetic energy (¹/₂ × mass × velocity²) can be used to find the resulting velocities for two colliding perfectly elastic objects. These two equations are used to determine the resulting velocities of the two objects. For the case of two balls constrained to a straight path by the strings in the cradle, the velocities are a single number instead of a 3D vector for 3D space, so the math requires only two equations to solve for two unknowns. When the two objects weigh the same, the solution is simple: the moving object stops relative to the stationary one and the stationary one picks up all the other's initial velocity. This assumes perfectly elastic objects, so there is no need to account for heat and sound energy losses.

One-dimensional Newtonian

In an elastic collision, both momentum and kinetic energy are conserved.^[1] Consider particles 1 and 2 with masses m₁, m₂, and velocities u₁, u₂ before collision, v₁, v₂ after collision. The conservation of the total momentum before and after the collision is expressed by:^[1]

m_{1}u_{1}+m_{2}u_{2}\ =\ m_{1}v_{1}+m_{2}v_{2}.

Likewise, the conservation of the total kinetic energy is expressed by:^[1]

{\tfrac {1}{2}}m_{1}u_{1}^{2}+{\tfrac {1}{2}}m_{2}u_{2}^{2}\ =\ {\tfrac {1}{2}}m_{1}v_{1}^{2}+{\tfrac {1}{2}}m_{2}v_{2}^{2}.

These equations may be solved directly to find $v_{1},v_{2}$ when $u_{1},u_{2}$ are known:^[2]

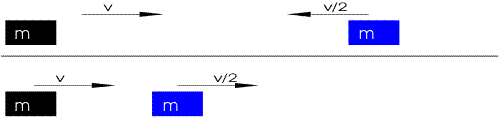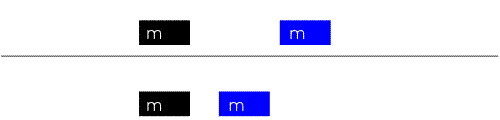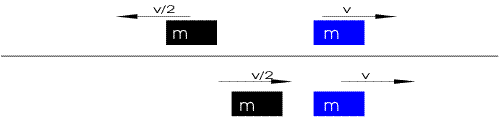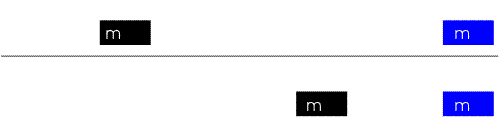
${\begin{array}{ccc}v_{1}&=&{\dfrac {m_{1}-m_{2}}{m_{1}+m_{2}}}u_{1}+{\dfrac {2m_{2}}{m_{1}+m_{2}}}u_{2}\\[.5em]v_{2}&=&{\dfrac {2m_{1}}{m_{1}+m_{2}}}u_{1}+{\dfrac {m_{2}-m_{1}}{m_{1}+m_{2}}}u_{2}\end{array}}$

If both masses are the same, we have a trivial solution:

v_{1}=u_{2}

v_{2}=u_{1}.

This simply corresponds to the bodies exchanging their initial velocities to each other.^[2]

As can be expected, the solution is invariant under adding a constant to all velocities (Galilean relativity), which is like using a frame of reference with constant translational velocity. Indeed, to derive the equations, one may first change the frame of reference so that one of the known velocities is zero, determine the unknown velocities in the new frame of reference, and convert back to the original frame of reference.

Examples

Ball 1: mass = 3 kg, velocity = 4 m/s

Ball 2: mass = 5 kg, velocity = −6 m/s

After collision:

Ball 1: velocity = −8.5 m/s

Ball 2: velocity = 1.5 m/s

Another situation:

Elastic collision of unequal masses.

The following illustrate the case of equal mass, $m_{1}=m_{2}$ .

Elastic collision of equal masses

Elastic collision of masses in a system with a moving frame of reference

In the limiting case where $m_{1}$ is much larger than $m_{2}$ , such as a ping-pong paddle hitting a ping-pong ball or an SUV hitting a trash can, the heavier mass hardly changes velocity, while the lighter mass bounces off, reversing its velocity plus approximately twice that of the heavy one.^[3]

In the case of a large $u_{1}$ , the value of $v_{{1}}$ is small if the masses are approximately the same: hitting a much lighter particle does not change the velocity much, hitting a much heavier particle causes the fast particle to bounce back with high speed. This is why a neutron moderator (a medium which slows down fast neutrons, thereby turning them into thermal neutrons capable of sustaining a chain reaction) is a material full of atoms with light nuclei which do not easily absorb neutrons: the lightest nuclei have about the same mass as a neutron.

Derivation of solution

To derive the above equations for $v_{1},v_{2}$ , rearrange the kinetic energy and momentum equations:

m_{1}(v_{1}^{2}-u_{1}^{2})=m_{2}(u_{2}^{2}-v_{2}^{2})

m_{1}(v_{1}-u_{1})=m_{2}(u_{2}-v_{2})

Dividing each side of the top equation by each side of the bottom equation, and using ${\tfrac {a^{2}-b^{2}}{(a-b)}}=a+b$ , gives:

v_{1}+u_{1}=u_{2}+v_{2}\quad \Rightarrow \quad v_{1}-v_{2}=u_{2}-u_{1}

That is, the relative velocity of one particle with respect to the other is reversed by the collision.

Now the above formulas follow from solving a system of linear equations for $v_{1},v_{2}$ , regarding $m_{1},m_{2},u_{1},u_{2}$ as constants:

\left\{{\begin{array}{rcrcc}v_{1}&-&v_{2}&=&u_{2}-u_{1}\\m_{1}v_{1}&+&m_{2}v_{2}&=&m_{1}u_{1}+m_{2}u_{2}.\end{array}}\right.

Once $v_{1}$ is determined, $v_{2}$ can be found by symmetry.

Newton's Cradle - Enery is always conserved somewhere

One-dimensional Newtonian

Examples

Derivation of solution

Related Videos